
Copyright
2015
Grade(s)
K - 2
Delivery Method
Blended (Print & Digital)
Imprint
Pearson Canada
Author(s)
Alex Lawson
READ
a wide variety of easy-to-implement activities and games that build children's number sense.
WATCH
how strategies and key ideas develop over time.
LISTEN
to narration that walks you through the learning.
 Play
Play
In this unique resource, teachers can watch, listen and read about the strategies and underlying key ideas that children use to solve problems. That’s because this is not just a book, but also an eText with 50+ narrated videos.
Author and researcher, Alex Lawson, tells the story of a group of students she interviewed and videotaped over several years. Through her narrative and video, you witness strategies and key ideas develop over time.
Good instruction is integral to developing student thinking and learning and this resources provides a wide variety of easy-to-implement classroom activities that build children’s number sense and early computation skills.
This resource was written in response to teacher requests. They wanted better insight into children’s mathematical development. This is the resource that will help them know:
“What does this child’s thinking tell me about what he or she understands?”
“Where does this child’s mathematical thinking lie on a framework of primary numeracy development?”
“What questions can I ask, or what activities can I do, to help this child move to the next phase?”
Note: What to Look For: Understanding & Developing Student Thinking in Early Numeracy eText licence duration is 99 months (8 years)
What to Look For 2: Understanding and Developing Student Thinking in Multiplicative Reasoning
Authors

Alex Lawson, Ph.D.
ALEX LAWSON, Ph.D., is Associate Professor of Education with Lakehead University’s Faculty of Education. A former elementary classroom teacher, she has been the director of the Multi-Data Convergence Lab at Lakehead University for the last decade, where hundreds of hours of children’s thinking have been documented and analyzed to improve elementary mathematical instruction and learning.
Resource Overview
We wrote this book in response to teachers’ requests. Teachers wanted better insight into children’s mathematical development. They wanted to know: “What does this child’s thinking tell me about what he or she understands?” “Where does this child’s mathematical thinking lie on a framework of primary numeracy development?” “What questions can I ask, or what activities can I do, to help this child move to the next phase?”
This resource is a sample video record of the mathematical development of 60 children over the course of two years. The teachers in the videos began with the children’s initial understandings and worked with their ideas to help the children develop increasingly sophisticated strategies and deepen their mathematical understanding. The development you see in these children is a result of this instruction.
Each chapter is organized around a series of video clips of interviews with children solving problems in a particular area of mathematics. These interviews were conducted over two and, occasionally, three years with the same children. The video icon, as shown in the margin, indicates that there is a video to be viewed. In chapters 2 to 5, the video is a snapshot of a time in a child’s mathematical development. In Chapter 6, it comprises several interviews with the same child, following a learning path from initial struggle through the development of increasingly sophisticated strategies.
This book is provided in print and eText format. To access the eText, see the information provided on the inside front cover of this book. Video clips can be viewed by clicking on the video icons in the eText.

Chapters 2 to 5 begin with a brief explanation of the strategies you will see children using in the videos, and the key ideas they are constructing. This introduction is followed by a brief discussion of the mathematical topics addressed in the chapter and children’s developing understandings of the topic. For each video, a chart describes what the child does during the interview and what this demonstrates about the child’s mathematical understanding. There are suggestions for assessing children’s development, sharing strategies in class discussions, and supporting children who are ready to try the strategy demonstrated or to construct the key idea implicit in the video. There may also be suggestions for what to do next with the children. Each chapter concludes with a chart that provides a brief explanation of the key ideas constructed by the children featured in the chapter.
Chapter 6 focuses on learning paths of particular children over a two-year period. Each child is developing a particular mathematical skill or key understanding. These children demonstrate learning paths that are representative of many we saw during our research.
The Teacher’s Math Kit, which follows Chapter 6, contains a selection of everyday living activities, mini-lessons, and games that can be used to support children as they develop the mathematical skills and understandings needed for number sense and early computation. These activities are referenced in the earlier chapters to indicate when they might best be used. Line masters, such as game boards, are provided for some activities. The line master icon, as shown in the margin, indicates when there is an activity master available for use.
View and download the line masters by clicking on the line master icons in the eText. You can access black line masters for the continua by clicking on the icons for MK22 and MK23.

Basic definitions of mathematical and instructional terms are provided in the margin the first time the terms are used in a chapter. The book also includes a reference section that lists the relevant scholarly articles and teacher resources referenced in the chapters.
How Can I Navigate Within the Book?
How you use and interact with the book will depend on your goals and situation. Although the text builds chronologically from early addition through to beginning multiplication and division strategies, it is not expected that you will read it in order from cover to cover. Here are just a few of the ways you may use this resource:
- Dip into several chapters to view videos as you look for ideas to help individual children in your class who are struggling todevelop a specific strategy or construct a specific key idea.
- Study one chapter in depth, perhaps as part of a professional learning group; you may even lead a group as it considers a topic such as the development of early addition and subtraction strategies.
- Read a chapter in preparation for introducing a new topic, such as multiplication, to your class.
- Follow the path of a child from initially struggling with a mathematical concept to gaining comprehension and mathematical proficiency.
All of these uses are possible, and they are aided by the detailed Chapter Overview of Videos charts. These charts, found in chapters 2 to 6, describe the problem being solved in each videotaped interview and identify the strategies and key ideas that can be seen or inferred from careful observation of the child as he or she works.
What Should I Do if the Vocabulary Is Unfamiliar to Me?
We expect the vocabulary to be new to you, and that expectation is part of the reason for writing the book. Deborah Ball, one of the most influential living mathematics educators today, makes the case that, as a profession, we do not achieve what we should with children, in part, because we do not have a common vocabulary of teaching. The most effective way to learn the new vocabulary is to approach it as you would when learning a new language: Use it. We encourage you to use the vocabulary in discussion with colleagues, administrators, and parents alike, as a way to solidify and refine your own understanding and capacity as a teacher of children’s mathematics.
Do I Need to Read the Book if the Vocabulary Is Familiar to Me?
Although most of our research team members were already familiar with the terminology, we still refined and solidified our thinking as we discussed the videos in order to write this book. Knowing the vocabulary provides you with a strong foundation, and maximizes the value of viewing the videos, reading this book, and discussing what you learn with others.
Can I Read the Book Without Viewing the Videos?
You could read this book and learn a great deal without looking at any of the videos. The description in each of the interview charts is a written record of what you would see in a given video. In this way, it is possible to use the book without viewing the videos. There may be times when you want to quickly access a given problem or strategy and do not have time to view the video. Having said that, there are aspects of the videos that we cannot capture in writing, so, at some point in your reading of the book, it would be worth viewing the videos.
How Do the Videos Enhance My Reading of This Book?
The videos will help you recognize, understand, and appreciate children’s thinking in your classroom. Alternatively, if you don’t see evidence of similar thinking in your class, the videos offer illustrations of children demonstrating this thinking. They will help you refine your understanding of a given strategy, and possibly the key ideas, because you see the first in action and may be able to infer the second. Finally, the videos will help you locate the strategies on the continuum we reference, supporting your ability to assess your learners’ mathematical knowledge and to plan for next steps.
How Can I Use This Resource in a Professional Development Situation to Support Teachers?
When I prepare to watch any of these videos with teachers in a professional development group, I first ask them to think about what they predict children might do to solve the given problem. They discuss their predictions with a partner, then watch the video. This helps prepare teachers to anticipate the wide range of strategies they may observe; further, they develop a common language and discuss what the video shows with a more critical and informed eye. Later, teachers often try out the problem with children in their own class to observe how they respond and to establish a basis for our next round of professional development.
What if I Were Thinking About Beginning Tomorrow?
Choose a problem from one of the chapters and develop a context that reflects the interests of the children in your class; for this first try, keep the numbers the same as in the sample problem. Use this problem as a “baseline.” At this point, resist the temptation to given the children too much support; look at what they know on their own. Compare their responses to what you see in the book. What strategies do you want to support your children in developing? Try out one of the games or activities suggested to foster a chosen strategy. Alternatively, try a new version of the same problem, this time changing the numbers, and have children discuss their strategies in a class debrief as the final part of the lesson. We turn now to the heart of the book: looking at children’s mathematics.
Developmental Continuum
Our Framework for Naming and Understanding Children’s Mathematical Thinking: Numeracy Continua of Addition and Subtraction and Multiplication and Division
In order to identify, understand, and assess children’s mathematical thinking, we have created two continua of numeracy development over time. Wherever possible, we drew on the existing theory and research to identify, infer, and label children’s behaviour and thinking.
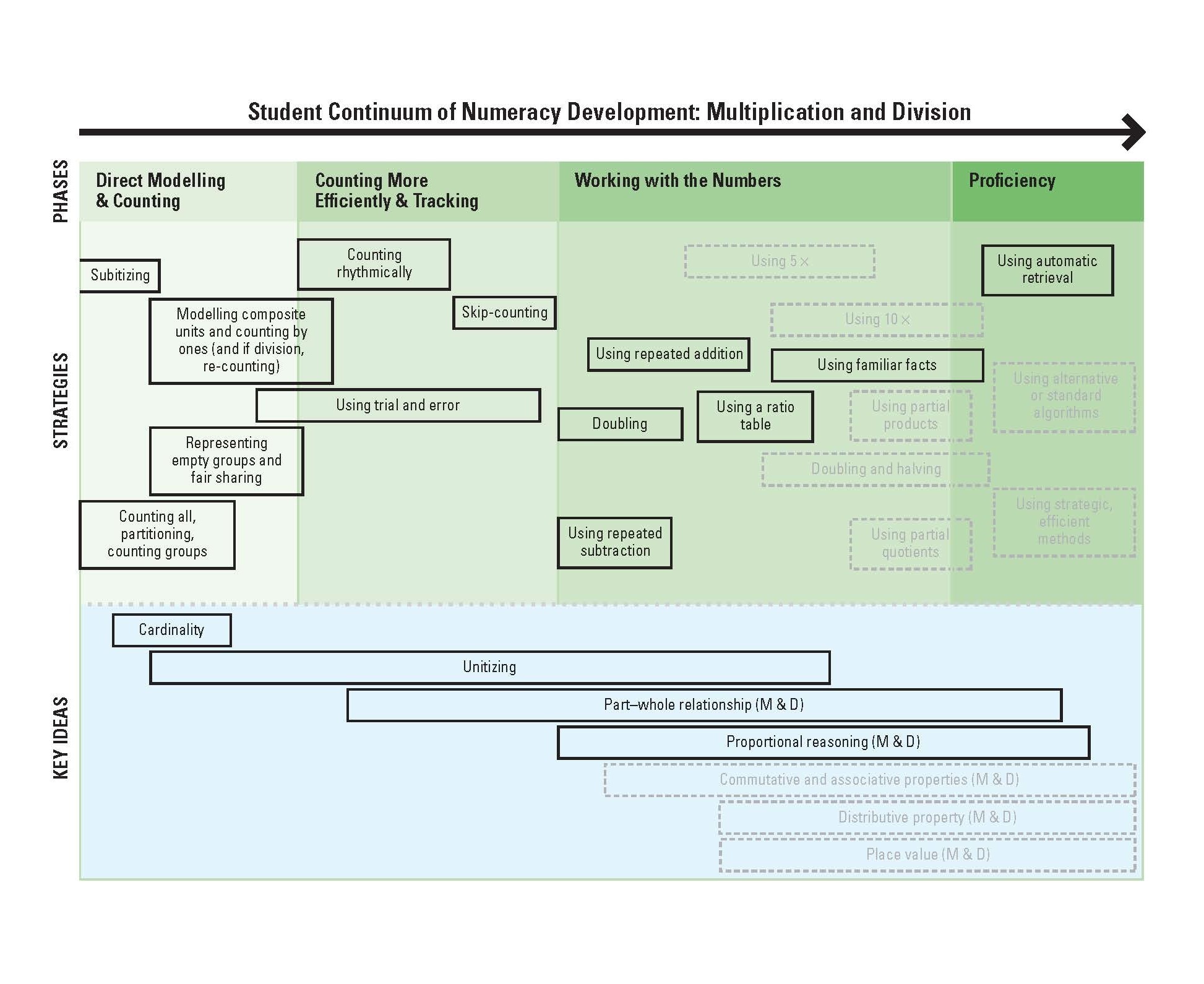
View the continuum for Multiplication and Division
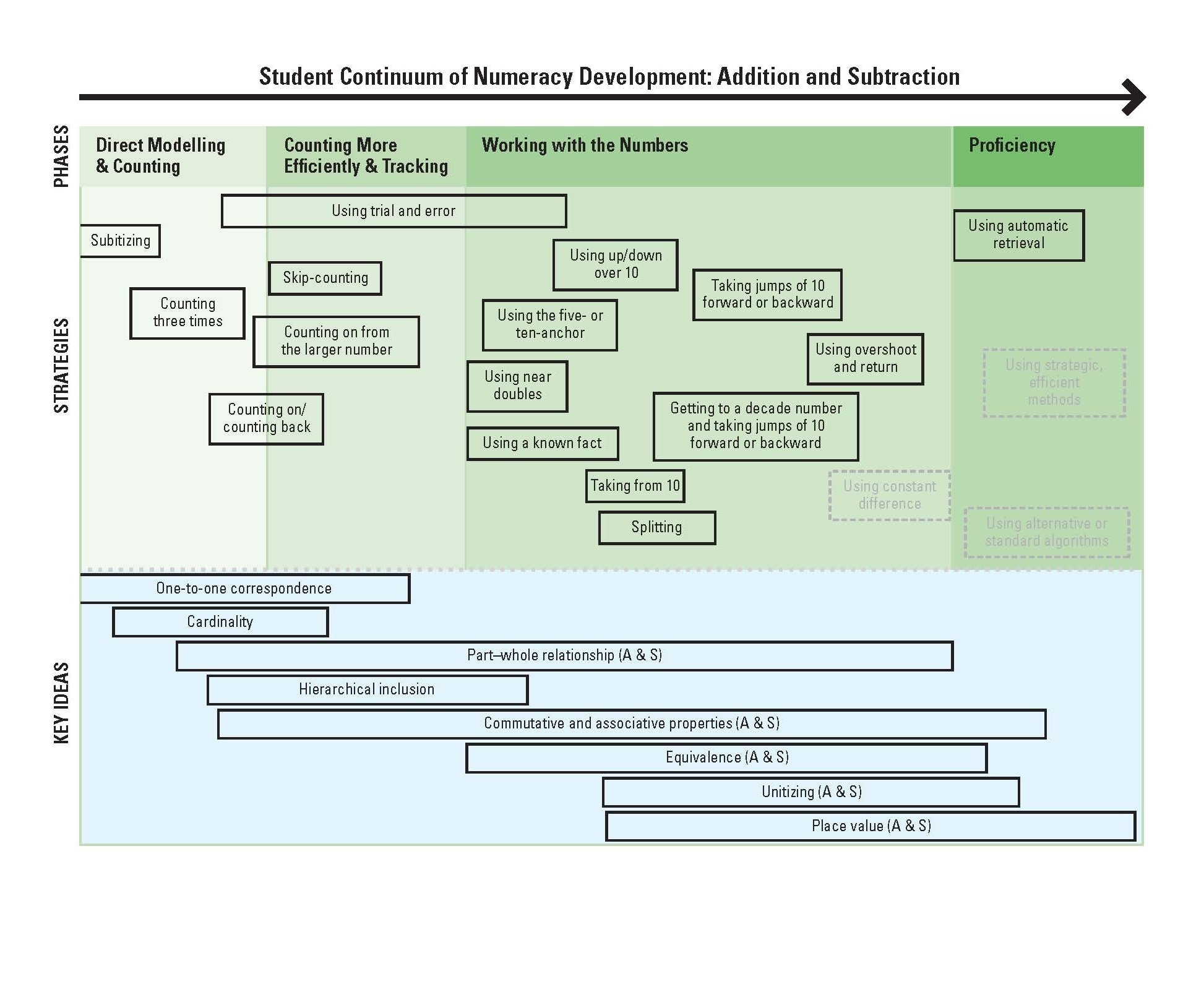
View the continuum for Addition and Subtraction
In particular, we identified and described the mathematical strategies—the actions, words, or written work children use to calculate or solve problems. We also labelled the key ideas we inferred they had, or were building, as they used a given strategy. We combined our field observations and inferences to create the Student Continuum of Numeracy Development: Addition and Subtraction and the Student Continuum of Numeracy Development: Multiplication and Division, which document children’s mathematical growth over time. The numeracy continua provide a graphic outline of this general progression, with the earliest strategies at the left, and the more efficient and complex ones at the right, while the inferred key ideas are shown across the bottom. Although there is an overall progression forward, the continua also document what we saw and what all observant teachers know: children’s mathematical progress is neither linear nor strictly developmental; instead, it jumps forward and backward and sometimes shifts laterally. The continua, therefore, allow for a variation in paths that the children in the videos took as they progressed mathematically. Finally, the continua are lenses through which teachers can view the mathematical development of children and can be used in classrooms to assess and plan for instruction.
What Terminology Do I Need to Know to Use This Resource
We make use of two overall terms in the continua of children’s mathematical development in numeracy:
- strategies
- key ideas
A strategy is what you hear and see as children work to solve a problem or to do a calculation. For example, suppose a child solves 5 + 7 by reversing the numbers, then raising 5 fingers as a physical model to be counted, putting each finger down while counting 8, 9, 10, 11, 12. The child is using the strategy of counting on from the larger number. The child is also demonstrating the use of knowledge you cannot see: a mathematical key idea.
While key ideas can have different meanings, we use the term narrowly, rather than broadly, to describe the important mathematical properties or ideas that children construct as they work with different strategies. The key ideas are not physically visible to us as teachers; instead we must infer them from the strategies we see children using. In this example, the child is making use of the commutative property: knowing that the order in which the numbers are added does not change the sum. In this case, the child has determined that 5 + 7 = 7 + 5. We can see that this child would have the mathematical power to add more disparate numbers, such as 5 + 11, by counting on. This child would only need to count on from 11 rather than from 5. Key ideas are therefore important. They can be roadblocks for children who have not yet constructed them (in this instance, labouriously counting on from 5 through 16) and mathematically powerful for those who have. While one might be tempted to try to teach key ideas directly, Kamii reminds us that, given effective instruction, children can “reinvent” them in order to do a calculation or to solve a problem.
The key ideas appear as bands across the bottom of each continuum. Each band spans a range of strategies, indicating when children first begin to develop the key idea through to when they have a solid understanding of it. For example, children may make use of the commutative property to count on from the larger number, to use a known fact, or to add up over 10. Children begin to construct the key ideas at somewhat different times in the two continua because multiplication and division key ideas are more complex. With multiplication and division, the child is dealing with relationships of multiple rather than single objects. These two terms provide the organizational backbone of this book.
Phases of Strategy Development
The strategies in each chapter are grouped into four general, increasingly sophisticated, phases of development on the continua:
- Direct Modelling & Counting
- Counting More Efficiently & Tracking
- Working with the Numbers
- Proficiency
When children use direct modelling strategies, they fully represent the problem with objects, then count the objects to find a solution. For example, to find 5 + 7, children would represent both numbers with objects, such as their fingers or marks on a page. As children shift to the next phase of development, they transition from direct modelling to tracking. With direct modelling, the objects children count are visible. When children shift to counting more efficiently & tracking, they may still use their fingers or marks on a page, but these are used to track their mental count. For example, to add 5 + = 12, children would track the missing addend as they count on from 5 to 12. Their 7 raised fingers would be a physical track of their mental count. When children shift to working with the numbers, they are no longer counting or tracking, but instead, operating on or with the numbers. For example, to add 5 + 7, they might decompose the 7 into 5 + 2 so they can add 5 + 5 to get 10, then add 2 more to get 12. When children achieve proficiency, they are demonstrating some or all of these strands of mathematical proficiency identified by the National Research Council.5 To paraphrase these strands, we can say that children:
- understand the mathematics they are using;
- are skillful, accurate, and fluent, choosing appropriate and efficient strategies;
- are able to communicate and justify their thinking and reasoning; and
- have a productive disposition, viewing mathematics as useful and believing in their own capacity to use it.
For example, children who have achieved proficiency not only know 5 + 7 = 12 as a “fact,” but they also understand the other relationships within this equation. For example, they know that 5 + 7 could be adjusted to get 6 + 6 = 12, or that the sum of 5 + 7 is 2 less than the sum of 7 + 7, or 2 more than the sum of 5 + 5, and so on. These children are able to communicate their thinking and justify why these other relationships are true. Furthermore, they have confidence in their ability to find the sum of 5 + 7 in another way if they momentarily forget their fact.
The phases of strategy development found on the continua are also displayed in The Interviews section of each chapter, on the side tabs, for quick access for assessment and teaching purposes.
Design Anatomy of the Continuum
The continuum captures the strategies in use and the underlying key ideas over the two grades we examined. Precursors (e.g., basic components of counting or the key idea of magnitude) could appear to the left of the figure if we had included kindergarten. Subitizing would also typically appear even before counting. We have nonetheless included it here because of its repeated use by children. You will notice several strategies that are delineated by broken lines. These broken lines represent strategies that we have yet to see in the videos but know will typically begin to appear in Grade 3. They have been included to show the full continuum of students’ early numeracy development.
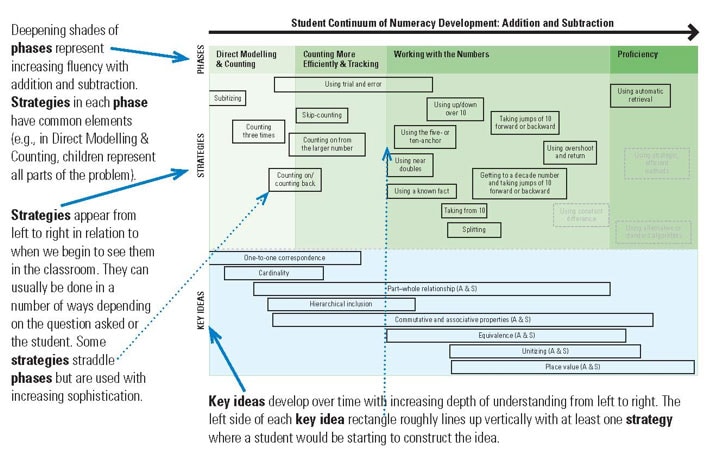
Table of Contents
Chapter 1
User’s Guide to What to Look For
Rationale
Using This Resource
The Beginning of the Continuum of Numeracy Development: Addition and Subtraction
Chapter 2
Addition and Subtraction to 20
What to Expect in the Chapter
How Primary Children Develop Addition and Subtraction Strategies
What to Expect in the Videos
Chapter Overview of Videos
The Interviews
Mathematical Key Ideas We Observed in This Chapter
Chapter 3
Varying Problem Types: Addition and Subtraction
What to Expect in the Chapter
The Structure of Addition and Subtraction Problems
Classifying Problem Types According to Their Structure
The Impact of Varied Problem Types
What to Expect in the Videos
Chapter Overview of Videos, Part 1
The Interviews
Chapter Overview of Videos, Part 2
The Interviews
Summary of Problem Types, Classified by the Location of the Unknown
Mathematical Key Ideas We Observed in This Chapter
Chapter 4
Addition and Subtraction over 20
What to Expect in the Chapter
How Primary Children Add and Subtract Multi-Digit Numbers
What to Expect in the Videos
Chapter Overview of Videos
The Interviews
Mathematical Key Ideas We Observed in This Chapter
Chapter 5
Early Multiplication and Division
What to Expect in the Chapter
Equal-Groups Multiplication and Division Problem Types
How Primary Children Solve Equal-Sets Grouping/Partitioning Problems
What to Expect in the Videos
Chapter Overview of Videos
The Interviews
Mathematical Key Ideas We Observed in This Chapter
Chapter 6
Learning Paths in Early Numeracy
What to Expect in the Chapter
What Do We Mean by a Learning Path?
What to Expect in the Videos
Chapter Overview of Videos
The Interviews
Teacher’s Math Kit
Classroom Activities to Support the Development of
Computational Proficiency
What to Expect in the Teacher’s Math Kit
Suggestions for Implementing Activities, Games, and Mini-lessons
Everyday Living Activities
Math Games & Activities
Mini-lessons
Conclusion
Appendices
References
How can I buy?

Purchase by Phone
Contact customer service at
1 (800) 361-6128


